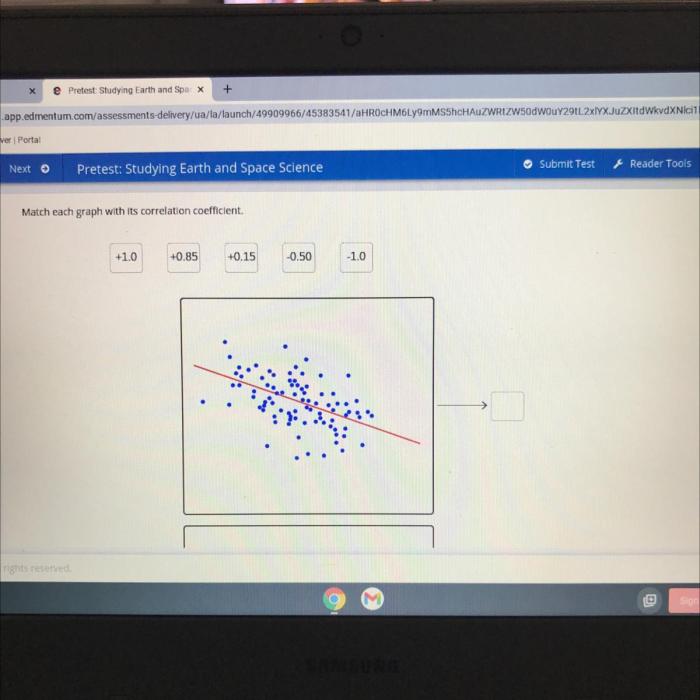
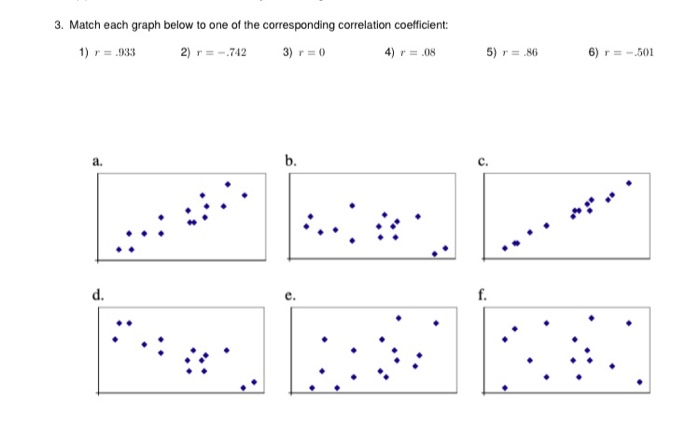
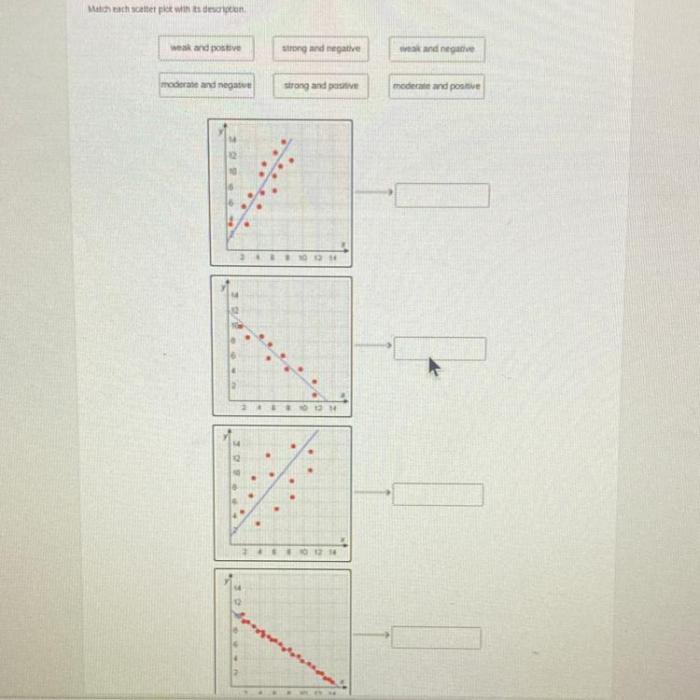
Match each graph with a description of its correlation. Correlation analysis is a statistical technique that measures the strength and direction of the relationship between two variables. It is a powerful tool that can be used to identify trends, make predictions, and understand the underlying relationships in data.
In this article, we will discuss the different types of correlation graphs and how to identify the correlation in each graph.
Correlation Analysis Overview: Match Each Graph With A Description Of Its Correlation.
Correlation analysis is a statistical technique used to measure the relationship between two or more variables. It determines the extent to which the changes in one variable are associated with changes in another variable. Understanding correlation is crucial for data analysis, as it helps researchers and analysts make informed decisions based on the data they collect.
There are different types of correlations:
- Positive correlation:Indicates that as one variable increases, the other variable also increases.
- Negative correlation:Indicates that as one variable increases, the other variable decreases.
- Strong correlation:Indicates a strong relationship between the variables, where changes in one variable are closely associated with changes in the other.
- Weak correlation:Indicates a weak relationship between the variables, where changes in one variable have little or no impact on the other.
Graph Types and Their Correlation
| Graph Type | Purpose | Correlation Representation | Example |
|---|---|---|---|
| Scatter Plot | Shows the relationship between two variables by plotting their data points on a graph. | Positive correlation: Points trend upwards from left to right. Negative correlation: Points trend downwards from left to right. | Analyzing the relationship between height and weight. |
| Line Graph | Displays data points connected by lines, showing trends over time or other continuous variables. | Positive correlation: Lines slope upwards. Negative correlation: Lines slope downwards. | Tracking sales figures over time. |
| Bar Graph | Compares different categories or groups of data using bars. | Positive correlation: Bars increase in height together. Negative correlation: Bars decrease in height together. | Comparing sales figures for different products. |
| Histogram | Shows the distribution of data by dividing it into bins and displaying the frequency of each bin. | Not typically used to represent correlation. | Analyzing the distribution of test scores. |
Identifying Correlation in Graphs
To identify correlation in graphs:
- Examine the overall trend:Look for patterns in the data points or lines.
- Determine the direction:Positive correlation (upward trend) or negative correlation (downward trend).
- Assess the strength:Strong correlation (closely aligned data points) or weak correlation (scattered data points).
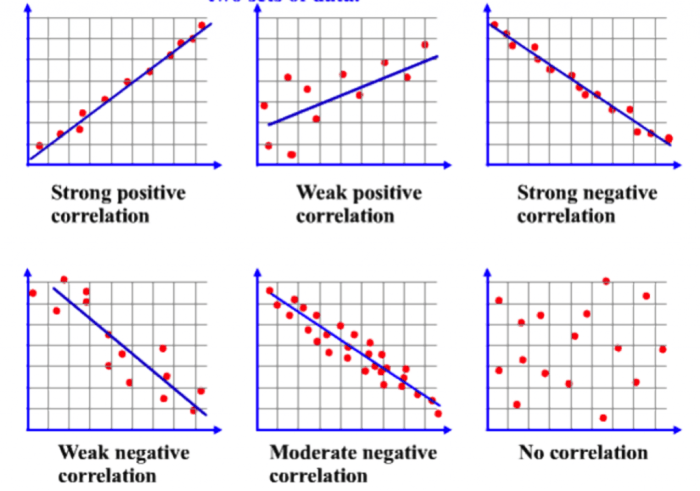
Visual Examples:
- Strong positive correlation:Data points form a straight line sloping upwards.
- Strong negative correlation:Data points form a straight line sloping downwards.
- Weak positive correlation:Data points form a scattered pattern trending upwards.
- Weak negative correlation:Data points form a scattered pattern trending downwards.
Correlation Analysis Methods
Common correlation analysis methods include:
- Pearson’s correlation coefficient (r):Measures linear correlation between two continuous variables.
- Spearman’s rank correlation coefficient (ρ):Measures monotonic correlation between two continuous or ordinal variables.
Advantages and Disadvantages:
- Pearson’s r:
- Advantages:Widely used, sensitive to linear relationships.
- Disadvantages:Assumes normality, affected by outliers.
- Spearman’s ρ:
- Advantages:Non-parametric, less affected by outliers.
- Disadvantages:Less sensitive to linear relationships.
Calculating Correlation:
- Pearson’s r:r = (Σ(x – x̄)(y – ȳ)) / √(Σ(x – x̄)²Σ(y – ȳ)²)
- Spearman’s ρ:ρ = 1 – (6Σd²) / (n³ – n)
Applications of Correlation Analysis
Correlation analysis has wide applications in various fields:
- Finance:Assessing the relationship between stock prices and economic indicators.
- Marketing:Identifying the correlation between advertising campaigns and sales.
- Healthcare:Determining the relationship between lifestyle factors and disease risk.
Benefits and Limitations:
- Benefits:
- Helps identify relationships between variables.
- Provides insights for decision-making.
- Limitations:
- Correlation does not imply causation.
- Can be affected by outliers and non-linear relationships.
Case Studies:
- A study found a strong positive correlation between exercise and improved cardiovascular health.
- A marketing campaign analysis revealed a positive correlation between social media engagement and product sales.
Top FAQs
What is correlation?
Correlation is a statistical measure that shows the relationship between two variables. It can be positive or negative, and it can be strong or weak.
What are the different types of correlation graphs?
There are four main types of correlation graphs: scatter plots, line graphs, bar graphs, and histograms.
How do I identify the correlation in a graph?
To identify the correlation in a graph, look at the shape of the data points. If the points are clustered together in a straight line, then there is a strong correlation. If the points are scattered all over the graph, then there is a weak correlation.