Unit 11 volume and surface area homework 5 – Embark on a mathematical journey through Unit 11: Volume and Surface Area, where we delve into the intricacies of calculating these fundamental properties for rectangular prisms, cylinders, and spheres. Our exploration will encompass formulas, real-world applications, and a comprehensive understanding of the concepts that underpin these geometric shapes.
Throughout this unit, we will unravel the mysteries of volume, the measure of the three-dimensional space occupied by an object, and surface area, the measure of the two-dimensional surface that bounds an object. By mastering these concepts, we empower ourselves to solve complex problems and gain a deeper appreciation for the world around us.
Volume of Rectangular Prisms
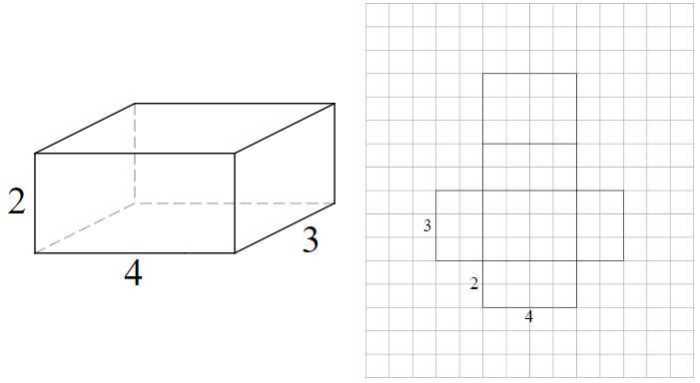
The volume of a rectangular prism is the amount of space it occupies. It is calculated by multiplying the length, width, and height of the prism. The formula for the volume of a rectangular prism is:
V = l × w × h
where:
- V is the volume in cubic units
- l is the length in units
- w is the width in units
- h is the height in units
Examples
- A rectangular prism with a length of 5 cm, a width of 3 cm, and a height of 2 cm has a volume of 5 cm × 3 cm × 2 cm = 30 cm 3.
- A rectangular prism with a length of 10 ft, a width of 8 ft, and a height of 6 ft has a volume of 10 ft × 8 ft × 6 ft = 480 ft 3.
Units of Volume
The most common unit of volume is the cubic unit, which is the volume of a cube with sides of length 1 unit. Other common units of volume include:
- cubic centimeter (cm 3)
- cubic meter (m 3)
- cubic foot (ft 3)
- gallon (gal)
To convert between different units of volume, use the following conversion factors:
- 1 m 3= 1000 cm 3
- 1 ft 3= 28.32 liters
- 1 gal = 3.785 liters
Surface Area of Rectangular Prisms
The surface area of a rectangular prism is the total area of all of its faces. It is calculated by adding the areas of all six faces. The formula for the surface area of a rectangular prism is:
SA = 2(lw + wh + hl)
where:
- SA is the surface area in square units
- l is the length in units
- w is the width in units
- h is the height in units
Examples
- A rectangular prism with a length of 5 cm, a width of 3 cm, and a height of 2 cm has a surface area of 2(5 cm × 3 cm + 3 cm × 2 cm + 2 cm × 5 cm) = 62 cm 2.
- A rectangular prism with a length of 10 ft, a width of 8 ft, and a height of 6 ft has a surface area of 2(10 ft × 8 ft + 8 ft × 6 ft + 6 ft × 10 ft) = 392 ft 2.
Units of Surface Area, Unit 11 volume and surface area homework 5
The most common unit of surface area is the square unit, which is the area of a square with sides of length 1 unit. Other common units of surface area include:
- square centimeter (cm 2)
- square meter (m 2)
- square foot (ft 2)
To convert between different units of surface area, use the following conversion factors:
- 1 m 2= 10,000 cm 2
- 1 ft 2= 0.0929 m 2
Questions and Answers: Unit 11 Volume And Surface Area Homework 5
What is the formula for calculating the volume of a rectangular prism?
Volume = length × width × height
How do I calculate the surface area of a cylinder?
Surface Area = 2πr(r + h)
What is the relationship between the radius and diameter of a sphere?
Diameter = 2 × radius