Embark on a mathematical journey with Big Ideas Math Geometry Chapter 11, where we delve into the fascinating realm of surface area and volume. From exploring the intricacies of prisms and cylinders to unlocking the secrets of pyramids and cones, this chapter promises an engaging and enlightening adventure.
Prepare to unravel the mysteries of three-dimensional figures, master the art of cross-sections, and discover the practical applications of surface area and volume in the world around us. Join us as we navigate the depths of geometry, unlocking its secrets and expanding our mathematical horizons.
Surface Area and Volume of Prisms and Cylinders: Big Ideas Math Geometry Chapter 11
In geometry, surface area and volume are two important concepts that measure the extent of three-dimensional objects. Surface area measures the total area of the surfaces of an object, while volume measures the amount of space it occupies.
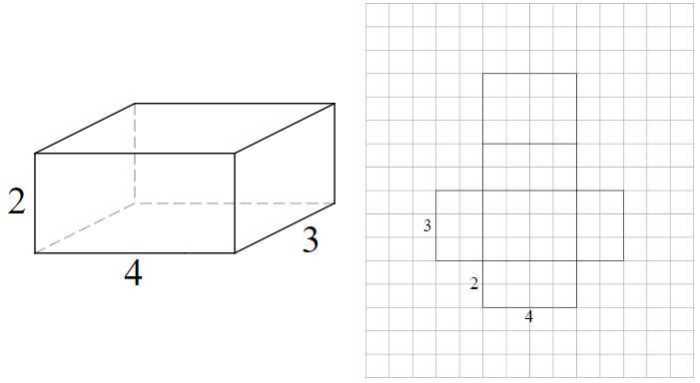
Surface Area and Volume of Rectangular Prisms
A rectangular prism is a three-dimensional shape with six rectangular faces. The surface area of a rectangular prism is the sum of the areas of all six faces. The volume of a rectangular prism is the product of its length, width, and height.
Formulas:
- Surface area = 2(lw + lh + wh)
- Volume = lwh
Surface Area and Volume of Cylinders
A cylinder is a three-dimensional shape with two circular bases and a curved surface. The surface area of a cylinder is the sum of the areas of the two bases and the curved surface. The volume of a cylinder is the product of the area of the base and the height.
Formulas:
- Surface area = 2πr(r + h)
- Volume = πr²h
The table below summarizes the formulas for calculating the surface area and volume of rectangular prisms and cylinders:
| Shape | Surface Area | Volume |
|---|---|---|
| Rectangular Prism | 2(lw + lh + wh) | lwh |
| Cylinder | 2πr(r + h) | πr²h |
Cross-Sections of Three-Dimensional Figures
In geometry, a cross-section is a two-dimensional figure that results from intersecting a three-dimensional figure with a plane. Cross-sections can be used to visualize the interior of a three-dimensional figure and to solve problems involving volume and surface area.
Types of Cross-Sections
There are three main types of cross-sections:
- Axial cross-sectionsare cross-sections that pass through the axis of symmetry of a three-dimensional figure.
- Equatorial cross-sectionsare cross-sections that pass through the equator of a three-dimensional figure.
- Oblique cross-sectionsare cross-sections that do not pass through the axis of symmetry or the equator of a three-dimensional figure.
Constructing Cross-Sections
To construct a cross-section of a three-dimensional figure, follow these steps:
- Draw the three-dimensional figure.
- Choose a plane to intersect the three-dimensional figure.
- Draw the intersection of the plane and the three-dimensional figure.
Using Cross-Sections to Solve Problems
Cross-sections can be used to solve a variety of problems, including:
- Finding the volume of a three-dimensional figure
- Finding the surface area of a three-dimensional figure
- Determining the shape of a three-dimensional figure
Surface Area and Volume of Pyramids and Cones
Pyramids and cones are three-dimensional figures with unique properties and applications. Understanding their surface area and volume is crucial for various fields, including architecture, engineering, and design. This section introduces the concepts of surface area and volume for pyramids and cones, derives their respective formulas, and presents a comparative table summarizing the formulas for prisms, cylinders, pyramids, and cones.
Surface Area of Pyramids, Big ideas math geometry chapter 11
The surface area of a pyramid is the total area of all its faces, including the base and the lateral faces. The base of a pyramid can be any polygon, such as a square, triangle, or pentagon. The lateral faces are triangles that meet at the vertex of the pyramid.
The formula for calculating the surface area of a pyramid is:“`Surface Area = Base Area + Lateral Surface Area“`where:
- Base Area is the area of the base polygon.
- Lateral Surface Area is the sum of the areas of all the lateral faces.
Volume of Pyramids
The volume of a pyramid is the amount of three-dimensional space it occupies. The formula for calculating the volume of a pyramid is:“`Volume = (1/3) x Base Area x Height“`where:
- Base Area is the area of the base polygon.
- Height is the distance from the vertex of the pyramid to the base.
Surface Area of Cones
A cone is a three-dimensional figure with a circular base and a single vertex. The surface area of a cone consists of the area of the circular base and the area of the lateral surface, which is a cone-shaped surface.
The formula for calculating the surface area of a cone is:“`Surface Area = Base Area + Lateral Surface Area“`where:
- Base Area is the area of the circular base.
- Lateral Surface Area = πrℓ, where r is the radius of the base and ℓ is the slant height (the distance from the vertex to the edge of the base along the lateral surface).
Volume of Cones
The volume of a cone is the amount of three-dimensional space it occupies. The formula for calculating the volume of a cone is:“`Volume = (1/3) x Base Area x Height“`where:
- Base Area is the area of the circular base.
- Height is the distance from the vertex of the cone to the base.
Comparative Table of Formulas
The following table summarizes the formulas for calculating the surface area and volume of prisms, cylinders, pyramids, and cones:| Figure | Surface Area | Volume ||—|—|—|| Prism | 2B + Ph | Bh || Cylinder | 2πrh + 2πr² | πr²h || Pyramid | Base Area + Lateral Surface Area | (1/3) x Base Area x Height || Cone | Base Area + πrℓ | (1/3) x Base Area x Height |
Applications of Surface Area and Volume
Surface area and volume are two essential concepts in geometry that have wide-ranging applications in the real world. These measurements play a crucial role in architecture, engineering, manufacturing, and even our everyday lives.
In architecture, surface area and volume determine the size, shape, and functionality of buildings. Architects use these measurements to calculate the amount of materials needed for construction, ensure adequate ventilation and lighting, and design spaces that are both aesthetically pleasing and practical.
Engineering
- Engineers rely on surface area and volume to design and build structures, machines, and systems. For example, in bridge design, the surface area of the bridge deck is crucial for determining the amount of weight it can support. Similarly, the volume of a fuel tank determines the amount of fuel it can hold.
- In the automotive industry, engineers use surface area and volume to optimize the aerodynamics and efficiency of vehicles. The shape and size of a car’s body affect its drag coefficient, which influences its fuel consumption.
Manufacturing
- Surface area and volume are critical factors in manufacturing processes. In the packaging industry, the surface area of a container determines the amount of material needed to produce it. The volume of a container, on the other hand, determines its capacity to hold products.
- In the food industry, the surface area of food products influences their rate of cooking, freezing, and dehydration. The volume of food products is also important for determining nutritional value and packaging requirements.
Everyday Life
Even in our everyday lives, surface area and volume play a role. The surface area of a pot or pan determines how quickly food cooks. The volume of a container determines how much liquid or food it can hold. The surface area of a room affects the amount of paint needed to cover its walls.
Understanding surface area and volume is essential for a wide range of professions and activities. These measurements provide valuable insights into the size, shape, and functionality of objects, enabling us to design, build, and interact with the world around us in a more informed and effective way.
Common Queries
What is the formula for calculating the surface area of a rectangular prism?
2(lw + lh + hw)
How do you find the volume of a cylinder?
πr²h
What is the difference between the surface area and volume of a pyramid and a cone?
A pyramid has a polygonal base, while a cone has a circular base. This difference affects the formulas used to calculate their surface area and volume.